![[인공지능][실습] 로지스틱 회귀(Logistic Regression) - 붓꽃 데이터(Iris Data)를 사용하여 3종류의 꽃을 분류해보자](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F4kxXC%2Fbtq40RqrP4Z%2FoGUwMpjNBFPOAnHgdRmf10%2Fimg.webp)
로지스틱 회귀(Logistic Regression)에 대한 이론이 필요하신 분들은 아래 링크를 참조해주시기 바랍니다.
[인공지능][개념] 로지스틱 회귀(Logistic Regression)는 무엇이며, 시그모이드(Sigmoid) 함수는 왜 사용하는 것일까? : https://itstory1592.tistory.com/8
[인공지능][실습] 로지스틱 회귀(Logistic Regression) - 나는 과연 타이타닉 침몰에서 살아남을 수 있었을까? : https://itstory1592.tistory.com/10
이번 시간에는 붓꽃 데이터(Iris Data)를 사용하여 로지스틱 회귀(Logistic Regression) 모델을 훈련하고,
꽃의 종류를 분류하는 실습을 진행해보도록 하자.
지난 글과는 다르게 이번 실습 데이터에서는 구분되는 경우의 수(클래스)가 3가지 이상이다.
이런 경우에는 시그모이드(Sigmoid) 함수가 아닌 소프트맥스(Softmax) 함수를 사용해야 한다.
우선 붓꽃 데이터(Iris Data)에 대해 간략히 알아보자.
아이리스(Iris) 데이터셋에는 3종류의 붓꽃 (setosa / versicolor / virginica) 데이터가 담겨져 있으며,
붓꽃 데이터의 특징(feature)에는 단위가 '센티미터(cm)인
'꽃받침 길이', '꽃받침 너비', '꽃잎 길이', '꽃잎 너비'
총 4가지로 구성되어 있다.
코드를 통해 더 구체적으로 살펴보자.
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np
우선, 모델을 훈련하기 위해 필요한 라이브러리(library)들을 임포트(import) 해준다.
편리하게도 사이킷런(sklearn)에서는 로지스틱 회귀 모델을 학습하기 위해 필요한
붓꽃 데이터를 가져올 수 있는 'datasets'을 제공해준다.
data = datasets.load_iris()
#데이터셋
input_data = data['data'] # 꽃의 특징 (input data)
target_data = data['target'] #꽃 종류를 수치로 나탄내 것 (0 ~ 2) (target data)
flowers = data['target_names'] # 꽃 종류를 이름으로 나타낸 것
feature_names = data['feature_names'] # 꽃 특징들의 명칭
#sepal : 꽃받침
#petal : 꽃잎
print('꽃을 결정짓는 특징 : {}'.format(feature_names))
print('꽃 종류 : {}'.format(flowers))
붓꽃 데이터를 가져오기 위해 datasets의 load_iris() 메소드를 호출하여 변수 data에 초기화해준다.
변수 data에는 여러 붓꽃 데이터에 대한 정보가 딕셔너리 형태로 저장되어 있는데,
input data로 사용할 데이터는 'data', target data로 사용할 데이터는 'target'이라는 key값으로 유지되어 있으므로
필요에 맞게 사용하면 된다.
해당 데이터에 대해 자세히 알아보기 위해, 꽃의 종류(species)와 특징(feature)으로 사용할 값에 대해서도 출력해보자.
초반에 설명한 '꽃받침 길이', '꽃받침 너비', '꽃잎 길이', '꽃잎 너비' 가
꽃의 종류를 구분하기 위한 데이터의 특징(feature)으로 잘 저장되어 있음을 확인할 수 있다.
꽃의 종류로는 setosa, versicolor, virginica라는 3가지 종류의 꽃들로 구성되어 있는 듯 하다.
(대체 무슨 꽃인지... 영알못..😅)
iris_df = pd.DataFrame(input_data, columns=feature_names)
iris_df['species'] = target_data
#맨 위에 있는 데이터 10개 출력
print(iris_df.head(10))
#데이터의 정보 출력
print(iris_df.describe())
다음으로는 판다스(pandas) 라이브러리에서 제공하는 데이터프레임(Dataframe)을 사용하여
각각의 변수에 담아놓았던 입력 데이터(input data)와 특징(feature)들을 보기 쉽게 맨 위부터 10개의 데이터를 출력해보자.
그리고, describe() 메소드를 통해 데이터에 대한 정보도 한 번 알아보자.
출력 결과, 맨 앞 10개의 데이터의 species가 0인 것을 통해
setosa라는 꽃에 대한 입력 데이터는 앞에 몰려있다는 것을 알 수 있다.
(확인해보니 총 데이터 300개 중, 앞 부분 100개는 setosa, 그 다음 100개는 versicolor, 뒷부분 100개는 virginica인듯 하다.)
그 밑에 출력된 것은 데이터의 개수, 평균, 표준편차, 최소ㆍ최댓값,
제 1사분위 (25%에 위치한 값), 제 2사분위 (중앙값, 50%에 위치한 값), 제 3사분위 (75%에 위치한 값)에 대한 정보이다.
이처럼, describe() 메소드를 사용하면 데이터의 대략적인 정보를 알 수 있다.
이제, 이 데이터를 seaborn 라이브러리를 통해 보기좋게 시각화 해보자.
#데이터 개괄적 특징 파악
sns.pairplot(iris_df, hue='species', vars=feature_names)
plt.show()
pairplot() 메소드의 pair에서 유추할 수 있듯이 2개의 변수가 쌍을 이루어 데이터를 2차원적으로 표현해주는데,
메소드에 첫번째 매개변수 데이터프레임을 입력하고,
매개변수 hue에는 시각화 하고자하는 변수를 입력하면 된다. 여기서는 타겟(target) 데이터인 species를 넣어준다.
매개변수 vars에는 입력 데이터(input data)인 특징(feature_names)을 입력한다.
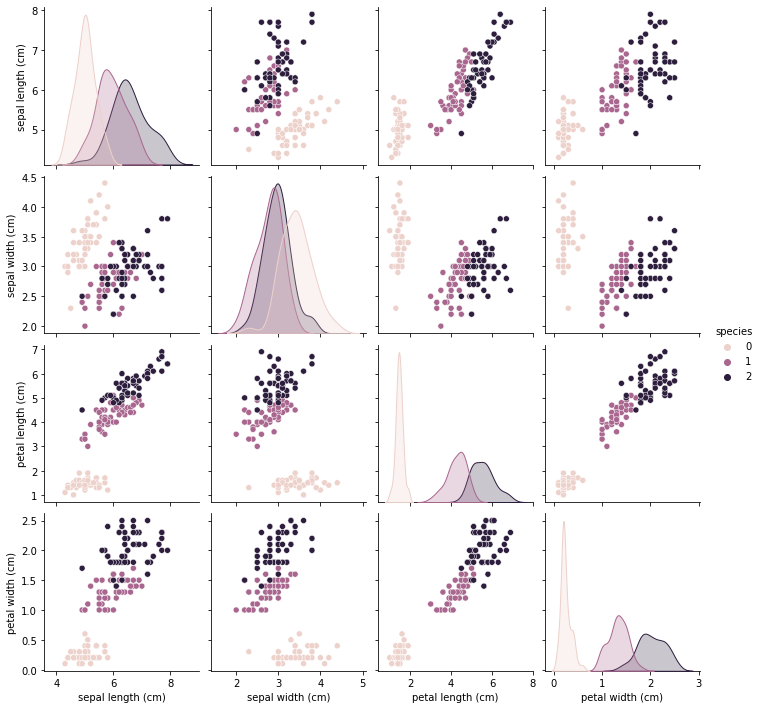
그럼, 이렇게 데이터에 대한 정보가 매개변수 hue에 입력한 species의 분포로 시각화된 그래프가 나타난다.
그래프를 보는법을 알아보기 위해 맨 좌측하단에 위치한 'sepal length와 petal width의 그래프'를 살펴보면,
'species 0'은 꽃받침 길이가 4~6cm 사이이며 꽃잎 너비가 0~0.5cm 사이이며,
'species 1'은 꽃받침 길이가 5~7cm 사이이며 꽃잎 너비가 1.0~1.5cm 사이임을 알 수 있다.
마지막으로, 'species 2'는 꽃받침 길이가 6~8cm 사이이며 꽃잎 너비가 1.5~2.5cm 사이라는 사실을 확인할 수 있다.
데이터를 시각화했을 때의 장점은, 각 변수 사이의 관계를 직접 눈으로 볼 수 있기 때문에
모델이 데이터를 분류하는 특징을 파악할 수 있다는 점이다. 👍
#훈련 데이터와 테스트 데이터 분리
train_input, test_input, train_target, test_target = train_test_split(
input_data, target_data, random_state=42)
#표준점수로 데이터 스케일링
scaler = StandardScaler()
train_scaled = scaler.fit_transform(train_input)
test_scaled = scaler.transform(test_input)
이제 본격적으로 모델을 학습시켜보자!
기존에 해왔던 것처럼, 훈련용 데이터와 테스트용 데이터로 input_data를 8:2 비율로 분리해준다.
또한, 각 특징(feature)들의 범위가 다르기 때문에, 훈련 과정에서 정확도가 떨어질 수 있다.
따라서 우리는 정확도를 조금이라도 높이기 위해 데이터를 전처리(Data Scaling) 할 필요가 있다.
여기에서는 StandardScaler 를 사용하여 각 데이터를 *표준점수로 변환시키도록 하겠다.
*표준점수 : 특정 값에 평균을 뺀 후, 표준편차로 나누어 정규화한 값
lr = LogisticRegression(max_iter=1000)
#로지스틱 회귀 학습
lr.fit(train_scaled, train_target)
#테스트 데이터 예측
pred = lr.predict(test_scaled[:5])
print(pred)
반복횟수(max_iter)를 1000으로 지정한 로지스틱 회귀모델을 생성하고,
훈련용 데이터셋으로 학습을 시킨 후, 테스트 데이터 5개에 대한 예측을 진행해보자.
출력 결과
[1 0 2 1 1]
내가 훈련시킨 모델은 테스트 데이터 5개를 위와 같은 값으로 예측하였다.
그렇다면 모델은 어떤 방식으로 예측을 한 것일까?
#로지스틱 회귀 모델의 가중치와 절편
#다중 분류 가중치와 절편을 출력하면, 각 클래스마다의 가중치 절편을 출력한다.
print(lr.coef_, lr.intercept_)
각 특징들의 가중치(weight)와 절편(bias)을 확인해보자.
모델은 3개의 클래스 (setosa, versicolor, virginica)들 중 확률이 가장 높은 하나를 예측 결과로 나타내는 것이기에
각 특징들(sepal_length, sepal_width, petal_length, petal_width)에 대한 3가지 클래스의 가중치(wieght)와 절편(bias)으로 구성되어 있다.
이 값들로 예측 확률을 구하기 위해 필요한 '방정식 Z'를 구할 수 있다.
예를 들어, 첫번째 배열이 setosa에 대한 가중치와 절편이므로 해당 값들로 식을 구성해보면,
setosa(z1) = (-0.96 * sepal_length) + (1.09 * sepal_width) + (-1.78 * petal_length) + (-1.66 * petal_width) - 0.39
라는 식으로 표현된다.
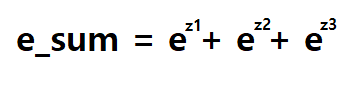
이런식으로 각 클래스들의 Z값을 모두 구한 후, 자연상수 e의 제곱으로 나타내어 모두 더한다. (= e_sum)
그리고 확률을 구하고 싶은 클래스의 e^z 을 전체 합으로 나누어주면,
해당 클래스의 확률이 되는 것이다. (= e^z / e_sum)
(위 식에서는 setosa의 확률을 구하는 식을 나타내 보았다.)
우리는 이런 방법으로도 Z값과 클래스의 확률을 구할 수 있지만,
사이킷런에서는 이런 번거로운 계산을 직접하지 않도록 decision_function()이라는 메소드를 제공해준다.
decision_function()을 호출하면 Z값을 알아서 구해준다.
#결정 함수(decision_function)로 z1 ~ z3의 값을 구한다.
decision = lr.decision_function(test_scaled[:5])
print(np.round(decision, decimals=2))
decision_function()에 테스트 데이터 5개를 넣고 소수점 2자리까지 출력해보면 위와 같은 결과가 출력된다.
5개의 데이터 이므로 5개의 배열이 출력되었으며, 3개의 클래스에 대한 Z값이 출력되었다.
예를 들어, 맨 왼쪽에 있는 값이 계산되는 과정을 알아보자.
맨 왼쪽은 setosa의 z값인데,
setosa(z1) = (-0.96 * sepal_length) + (1.09 * sepal_width) + (-1.78 * petal_length) + (-1.66 * petal_width) - 0.39
이 식에 있는 변수 (sepal_length, sepal_width, petal_length, petal_width) 에 테스트 데이터 5개를 대입하면,
setosa의 z값 5개 (-2.21, 5.87 -9.33 -2.29, -3.59) 가 계산된다.
위에서 설명한 것처럼, 이 z값으로 직접 확률을 구할 필요가 없다.
#소프트맥스 함수를 사용한 각 클래스들의 확률
from scipy.special import softmax
proba = softmax(decision, axis=1)
print(np.round(proba, decimals=3))
decision_function()을 통해 구한 값을 scipy에서 제공하는 softmax 함수에 전달해주면
각 클래스에 대한 확률을 구해주기 때문이다.
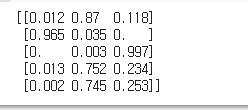
아까 모델이 예측한 결과값 [1 0 2 1 1] 과 비교해보면,
첫번째는 데이터는 87%의 확률로 1(versicolor)이라고 예상했고,
두번째 데이터는 97%확률로 0(setosa)이라고 예상했다.
나머지 데이터도 동일하게 가장 확률이 높은 것을 예측 결과값으로 내놓을 것이다.
오늘은 로지스틱 회귀(Logistic Regression)를 통해 붓꽃을 구분하는 모델을 구현해보았다.
단순히 두가지 클래스로 분류할 때 사용했던 시그모이드(Sigmoid) 함수와 다르게, 분류해야 할 클래스가 세가지 이상이 됐을 때는 소프트맥스 (Softmax) 함수를 사용해야 한다는 것을 알게 되었다.
또한, 확률을 구하기 위한 z값을 결정함수(decision function)를 통해 계산할 수 있었으며,
해당 값을 소프트맥스(softmax) 함수에 전달하여 확률을 얻어내는 과정을 직접 확인해보았다.
전체 소스 코드 :
https://colab.research.google.com/drive/190hj8x41nm22hDimOsVc21vT7uwUkSzt?hl=ko
(이해가 다소 힘들거나, 틀린 부분이 있다면 댓글 부탁드리겠습니다! 😊)
💖댓글과 공감은 큰 힘이 됩니다!💖