[인공지능][실습] 다항회귀(Polynomial Regression)와 다중선형회귀(Mutiple Linear Regression)를 활용하여 생선의 무게를 예측해보자

 

 

(아직 이론에 대한 글을 읽지 않았다면, 아래의 링크를 참고하는 것을 추천👍)

[인공지능][개념] 다항회귀(Polynomial Regression)와 다중선형회귀(Mutiple Linear Regression) + 규제(Regularization)에 대해 알아보자 : itstory1592.tistory.com/6

 

 

 

다항회귀와 다중선형회귀를 통해 정확도를 높여보자!

 

 

지난 글에서 다항회귀 (Polynomial regression)과 다중선형회귀 (Multiple linear regression)에 대한 이론을 알아보았다.

이번에는 이론으로만 공부한 두 개념을 적용하여 선형회귀보다 조금이라도 더 정확히 생선의 무게를 맞출 수 있는

모델을 만들어보도록 하자.

 

 

'생선 데이터의 그래프'

 

지난 이론에서 설명하였듯이, 사실 생선 데이터의 분포를 그래프로 표현했을 때,

1차 방정식보다는 2차 방정식의 곡선과 유사하게 그려진다고 설명하였다.

따라서, 단일 선형회귀가 아닌 다항 선형회귀를 사용하면서,

데이터의 특징(feature)을 몇 가지 더 추가하여 조금 더 디테일한 모델을 만들어보자.

 

 

---

 

 

import pandas as pd

df = pd.read_csv('https://bit.ly/perch_csv_data')
perch_full = df.to_numpy()

#길이 높이 너비
print('길이\t높이\t너비')
print(perch_full)

 

import numpy as np

#농어의 무게
perch_weight = np.array(
    [5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 
     110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 
     130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 
     197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 
     514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 
     820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 
     1000.0, 1000.0])

 

이전에는 데이터를 모두 직접 선언하였지만,

편의를 위해 한빛미디어에서 제공해주는 농어의 데이터를 pandas 라이브러리로 불러오자.

농어의 무게는 타겟(target) 데이터이므로 직접 선언하였다.

 

해당 데이터에는 길이, 높이, 너비라는 3가지 특징으로 이루어져있어 다중선형회귀를 구현할 수 있다.

 

 

from sklearn.model_selection import train_test_split

# 훈련 세트와 테스트 세트로 나눕니다
train_input, test_input, train_target, test_target = train_test_split(perch_full, perch_weight
, test_size=0.2, random_state=42)

print(train_input.shape[0], test_input.shape[0])

 

그런 다음, 나중에 모델을 테스트하기 위해, 데이터를 훈련세트와 테스트세트로 각각 80% 20%의 비율로 나누어 주었다.

맨 마지막 줄의 코드를 실행시켜보면 44개 12개로 적절히 나누어진 모습을 확인할 수 있다.

 

 

from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures()
poly.fit([[2, 3]])

print(poly.transform([[2, 3]]))

 

데이터를 적절히 나누어 주었다면 해당 데이터를 다항(Polynomial)으로 나타내기 위해,

사이킷런(sklearn)에서 제공해주는 PolynomialFeatures라는 클래스를 임포트 해준다.

 

해당 클래스를 사용하면 자동으로 데이터를 다항식으로 변형시켜주는데, 클래스를 선언해주고 이전 시간에 선형회귀 모델을 훈련시킬 때 사용했던 것처럼 fit() 메소드를 호출해준다.

이 경우, 데이터 리스트를 2차원 형태로 입력해준 후 transform() 메소드를 호출하면 아래와 같은 결과를 확인할 수 있을 것이다.

 

 

[[1. 2. 3. 4. 6. 9.]]

 

PolynomialFeatures()에는 degree라는 매개변수로 최대 몇 차식까지 변형시킬지를 설정할 수 있는데,

degree의 기본 값은 2이므로, 2의 제곱, 3의 제곱 그리고 서로를 곱한 값으로 변형된 것을 확인할 수 있다.

 

 

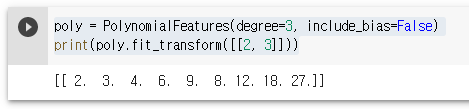
poly = PolynomialFeatures(degree=3, include_bias=False)
print(poly.fit_transform([[2, 3]]))

 

만약 3차식으로 표현하면서 bias를 제외하고 싶다면

degree를 3으로, include_bias를 False로 설정하면 된다.

또한, 해당 값에 맞춰 훈련시킴과 동시에 변형까지 시키고 싶다면 fit과 transform을 따로 쓰는 대신에

fit_transform() 메소드를 호출시켜주면 된다.

 

 

degree를 3으로 설정하여 최대 3제곱까지 변형된 결과값

 

PolynomialFeatures 클래스에 대한 이해가 끝났다면, 바로 생선에 대한 데이터를 변형시켜보자.

 

 

#PolynomailFeatures() 를 적용하기 전의 데이터 형태
print("Not poly train data : {} / Not poly test data : {}".format(train_input.shape, test_input.shape))

poly = PolynomialFeatures(include_bias=False)

train_poly = poly.fit_transform(train_input)
test_poly = poly.transform(test_input)

#PolynomialFeatures() 를 적용한 후의 데이터 형태
print("Poly train data : {} / Poly test data : {}\n".format(train_poly.shape, test_poly.shape))

변형 전 데이터와 변형 후 데이터의 형태

 

위 코드의 결괏값을 확인해보면 3가지였던 특성이 9개의 특성으로 변형되었음을 알 수 있다.

 

 

#Polynomial data shape
poly.get_feature_names()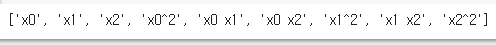

최대 2의 제곱으로 변형된 데이터

 

추가적으로, get_feature_names()라는 메소드를 호출하면 데이터가 어떤 식으로 변형되었는지도 확인할 수 있다.

x0 x1 x2는 각각 생선의 길이 높이 너비를 표현한 것이고 degree는 2로 자동 설정되어 있으므로,

최대 2의 제곱으로 변형된 것이다.

 

 

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(train_poly, train_target)

#훈련 데이터의 정확도
print(lr.score(train_poly, train_target))
#테스트 데이터의 정확도
print(lr.score(test_poly, test_target))

 

그렇다면 변형된 데이터(train_poly)를 사용하여 모델을 훈련시켜보자.

그런 다음 훈련 데이터와 테스트 데이터의 정확도를 확인해보면

 

 

Polynomial Featrue을 사용하여 변형된 데이터로 훈련한 모델의 정확도

 

Wow..!! 😃

훈련 데이터와 테스트 데이터 모두 정확도가 확연하게 상승한 것을 확인할 수 있으며

과대적합(Overfitting)도 어느 정도 해결한 것으로 보입니다.

 

degree를 더 높인다면 거의 100%에 가까운 모델을 만들 수 있지 않을까 하는 희망이 들게 만드는 결과이다.

바로 테스트해보자.

 

 

poly = PolynomialFeatures(degree=5, include_bias=False)
train_poly = poly.fit_transform(train_input)
test_poly = poly.transform(test_input)

#최대 차수가 5인 데이터를 훈련시킨다.
lr.fit(train_poly, train_target)

#훈련 데이터의 정확도
print(lr.score(train_poly, train_target))
#테스트 데이터의 정확도
print(lr.score(test_poly, test_target))

 

degree를 5로 변경하여 차수를 최대 5인 데이터로 변형시킨 후 훈련을 진행하고, 바로 정확도를 출력해보았다.

결과는?!

 

 

훈련 데이터의 정확도는 100%의 확률에 가까워졌지만,

테스트 데이터의 정확도는 -167이라는 말도 안 되는 수치가 출력되었다.

이게 어떻게 된 일일까?!

 

 

앞서 이론에서 설명하였듯이, 특성이 적절하게 많다면 모델의 정확도가 높아지지만,

반대로 특성의 개수가 과도하게 많아지면 과대적합(Overfitting)이 발생할 수도 있다고 설명하였다.

 

이 또한 마찬가지로 예를 들자면,

여러분들이 누군가에게 정답을 맞혀 보라고 하고 문제를 내고, 힌트로 정답의 특징을 너무 광범위하게 설명하여

오히려 정답을 맞히는 데에 있어 상대방을 헷갈리게 만든 상황이 되어버린 것이다.

 

그렇다면 이런 문제는 어떻게 해결할 수 있을까?

 

 

규제 (Regulation)

---

 

사이킷런(sklearn)은선형회귀에서 이러한 상황을 해결할 수 있는 유용한 규제 클래스를 제공해준다.

바로 릿지(Ridge) 라쏘(Lasso)라는 클래스이다.

이 규제 클래스들은 너무 많은 특징을 제공하는 경우에 있어,

'이제 그만! 너무 특징이 많아서 헷갈려! 이 정도면 충분해😊'

라고 말하며 자동으로 특징의 개수를 적절하게 규제해주는 역할을 한다.

릿지는 다른 말로 L2규제 / 라쏘는 L1규제로 불리기도 한다.

이 둘은 비슷해 보이지만, 당연하게도 차이점이 존재한다.

 

릿지(Ridge)의 경우, 변형된 데이터 변수를 모두 사용하되, 계수를 줄이는 방식을 사용하고,

라쏘(Lasso)의 경우, 일정 변수들의 계수를 0으로 만들어 사용하지 않도록 하는 방법을 택한다.

따라서, 라쏘를 사용하면 데이터가 손실되어 정확도가 떨어지는 위험성이 있기도 하다.

 

 

 

그럼 바로 이 두 규제방식을 코드로 구현해보도록 하자.

 

from sklearn.preprocessing import StandardScaler

#데이터 전처리
#기본 스케일러, 평균과 표준편차를 사용
ss = StandardScaler()
ss.fit(train_poly)

train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)

 

우선, StandardScaler 클래스를 임포트 하여 데이터를 전처리시켜주자.

데이터전처리(Preprocessing)를 하면 각 특징(feature)의 범위가 다를 수도 있는 경우를 방지하여 정확도를 더 높일 수 있다.

 

예를 들어, 생선의 길이는 20~50cm이지만, 생선의 너비는 2~6cm 정도밖에 되지 않아

각 데이터의 범위의 차이로 정확도가 떨어질 수 있는데,

이를 표준점수로 변환하여 비슷한 범위 내에서 데이터를 처리하면 정확도를 높일 수 있기 때문이다.

StandardScaler도 이전과 마찬가지로 fit()과 transform() 메소드를 사용하여 표준점수로 변형시키면 된다.

 

릿지(Ridge)부터 사용해보자!

 

 

from sklearn.linear_model import Ridge

#릿지
ridge = Ridge()
ridge.fit(train_scaled, train_target)

#훈련 데이터의 정확도
print(ridge.score(train_scaled, train_target))
#테스트 데이터의 정확도
print(ridge.score(test_scaled, test_target))

 

릿지회귀도 단순하게 기존 선형회귀처럼 사이킷런(sklearn)의 Ridge 클래스를 임포트하면 된다.

그렇게, 생성한 ridge를 전처리한 데이터셋으로 훈련을 시킨 후,

훈련 데이터셋과 테스트 데이터셋의 정확도를 출력해보도록 하자.

 

 

릿지(Ridge)회귀에서의 훈련 데이터셋과 테스트 데이터셋의 정확도

 

놀랍게도 마이너스(-)에서 맴돌던 테스트셋의 정확도가 97%까지 상승하였다.

위에서 설명했듯이, L2규제를 통해 변수의 계수를 줄인 결과이다.

 

Ridge() 클래스에는 alpha라는 매개변수를 통해 이를 조절할 수 있는 하이퍼 파라미터(Hyper Parameter)가 존재한다.

0.001 ~ 100까지 값을 조절해가며, 최적의 alpha값을 찾아보자.

 

 

import matplotlib.pyplot as plt

train_score = []
test_score = []

alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
    # 릿지 모델을 만듭니다
    ridge = Ridge(alpha=alpha)
    # 릿지 모델을 훈련합니다
    ridge.fit(train_scaled, train_target)
    # 훈련 점수와 테스트 점수를 저장합니다
    train_score.append(ridge.score(train_scaled, train_target))
    test_score.append(ridge.score(test_scaled, test_target))

 

alpha_list라는 변수에 0.001부터 100까지 alpha값을 저장하고,

for 반복문을 통해 순차적으로 ridge를 훈련하며 점수를 기록해보자.

기록한 훈련 점수와 테스트 점수는 train_score와 test_score 배열에 추가(append)하도록 되어 있다.

 

 

plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()

 

for 반복문이 끝났다면, 맷플롯립(matplotlib) 라이브러리에서 제공하는 plot() 메소드로 각 점수를 그래프로 나타내 보자.

이때, 넘파이에서 제공하는 log10() 메소드로 결과 값을 변환하여 나타낸다.

ex) 0.001 = 10^-3 = -3

 

 

훈련 점수와 테스트 점수의 결정계수(R^2)와 alpha값으로 나타낸 그래프

 

R^2는 결정계수라고 불리며 1에 가까울수록 정확도가 높다는 뜻으로 해석하면 된다.

그래프에서, alpha가 1 (10^1)일 때, 테스트 점수와 훈련 점수 사이의 차이가 적으면서, 결정계수까지 높으므로

이 모델에서 최적의 alpha값은 10이라는 사실을 알 수 있다.

 

릿지(Ridge)에 대해서 알아보았으니, 라쏘(Lasso)에 대해서도 알아보자.

 

 

from sklearn.linear_model import Lasso

lasso = Lasso()
lasso.fit(train_scaled, train_target)

print(lasso.score(train_scaled, train_target))
print(lasso.score(test_scaled, test_target))

 

위 코드에서 Ridge를 Lasso로 바꾸기만 하면 된다.

Lasso 또한, 동일하게 높은 점수를 보여주므로 결과는 생략하도록 하겠다.

 

 

train_score = []
test_score = []

alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
    # 라쏘 모델을 만듭니다
    lasso = Lasso(alpha=alpha, max_iter=10000)
    # 라쏘 모델을 훈련합니다
    lasso.fit(train_scaled, train_target)
    # 훈련 점수와 테스트 점수를 저장합니다
    train_score.append(lasso.score(train_scaled, train_target))
    test_score.append(lasso.score(test_scaled, test_target))

 

마찬가지로, ridge를 lasso로 변경해주기만 하면 된다.

대신 max_iter라는 파라미터가 등장하는데, 반복하는 최대 횟수를 지정하는 변수이다.

여기서는 10000으로 설정하여 테스트해보겠다.

 

 

plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()

 

 

라쏘(Lasso) 또한 마찬가지로 alpha가 10일 때, 가장 높은 점수를 기록하였다.

라쏘는 계수를 0으로 만들어 과대적합(Overfitting)이나 과소적합(Underfitting)을 해결한다고 했는데,

그렇다면 몇개의 특징(feature)의 계수를 0으로 만들었는지 확인해보며 마무리 하도록 하겠다.

 

 

#사용되지 않는 특징의 개수
print(np.sum(lasso.coef_ == 0))

결과 값 : 53

 

결과 값으로 53이 출력되었다.

lasso 모델의 계수를 출력하는 coef_변수에서 계수가 0인 갯수를 합하는 코드인데,

결과가 이렇게 출력되었다는 것은 0으로 변경된 계수가 총 53개라는 뜻이다.

 

 

이번 글에서는 다항회귀(Polynomial Regression)와 다중선형회귀(Multiple Linear Regression),

그리고 릿지(Ridge)와 라쏘(Lasso)를 이용한 규제(Regulation)를 직접 다루어보았다.

차수가 너무 높은 경우 과대적합이 일어날 수 있는데, 규제를 통해 모델을 제어하며 정확도를 높여보았다.

다음 글에서는 로지스틱 회귀(Logistic Regression)를 알아볼 예정이다.

 

 

 

(이해가 다소 힘들거나, 틀린 부분이 있다면 댓글 부탁드리겠습니다! 😊)

💖댓글과 공감은 큰 힘이 됩니다!💖