
https://www.acmicpc.net/problem/1003
1003번: 피보나치 함수
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
www.acmicpc.net
문제
다음 소스는 N번째 피보나치 수를 구하는 C++ 함수이다.
int fibonacci(int n) {
if (n == 0) {
printf("0");
return 0;
} else if (n == 1) {
printf("1");
return 1;
} else {
return fibonacci(n‐1) + fibonacci(n‐2);
}
}fibonacci(3)을 호출하면 다음과 같은 일이 일어난다.
- fibonacci(3)은 fibonacci(2)와 fibonacci(1) (첫 번째 호출)을 호출한다.
- fibonacci(2)는 fibonacci(1) (두 번째 호출)과 fibonacci(0)을 호출한다.
- 두 번째 호출한 fibonacci(1)은 1을 출력하고 1을 리턴한다.
- fibonacci(0)은 0을 출력하고, 0을 리턴한다.
- fibonacci(2)는 fibonacci(1)과 fibonacci(0)의 결과를 얻고, 1을 리턴한다.
- 첫 번째 호출한 fibonacci(1)은 1을 출력하고, 1을 리턴한다.
- fibonacci(3)은 fibonacci(2)와 fibonacci(1)의 결과를 얻고, 2를 리턴한다.
1은 2번 출력되고, 0은 1번 출력된다. N이 주어졌을 때, fibonacci(N)을 호출했을 때, 0과 1이 각각 몇 번 출력되는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다.
각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. N은 40보다 작거나 같은 자연수 또는 0이다.
출력
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
예제 입력 / 예제 출력
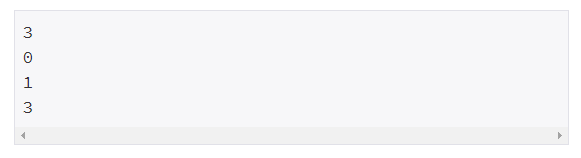 |
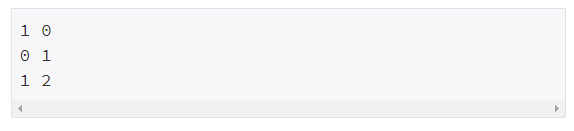 |
문제 풀이
전체 소스 코드 보기
zero = [1, 0, 1]
one = [0, 1, 1]
def fibonacci(num):
length = len(zero)
if num >= length:
for i in range(length, num+1):
zero.append(zero[i-1] + zero[i-2])
one.append(one[i-1] + one[i-2])
print('{} {}'.format(zero[num], one[num]))
T = int(input())
for _ in range(T):
fibonacci(int(input()))
이 문제는 다이나믹 프로그래밍을 통해 피보나치에서 호출되는 0과 1을 카운팅 하는 문제이다.
재귀 함수로만 문제를 풀려고 하면 시간 제한으로 인해 오답 처리되기 때문이다.
여기서 피보나치(Fibonacci) 함수란 '한 단계 전의 숫자와 두 단계 전의 숫자를 더하는 함수'이다.
일부 숫자에 대한 피보나치 표를 아래에 간단히 정리하였다.
| 숫자 | 0 | 1 | 2 | 3 | 4 | 5 |
| 피보나치 (fibonacci) |
0 | 1 | 1 | 3 | 5 | 7 |
표를 확인해보면, 숫자가 0과 1인 경우에는 두 단계 이전의 숫자가 존재하지 않기 때문에 그 숫자 자체로 피보나치가 적용된 역할을 한다.
* (fibonacci(0) = 0 / fibonacci(1) = 1)
fibonacci(2)부터는 그 이전 피보나치 숫자인 fibonacci(1)과 fibonacci(0)을 더하여 1이라는 값을 갖는다.
그다음 fibonacci(3)은 fibonacci(2)에서 구한 값 1과 fibonacci(1)의 값을 더해 1이라는 결과를 얻을 수 있다.
그 이후의 숫자들도 피보나치 함수를 적용하면 모두 동일한 과정을 이룬다.
하지만 문제를 읽어보면 알다시피 피보나치 값을 구하는 것이 아닌, 특정 값의 피보나치를 구하기 위해서 호출되는
fibonaaci(0)과 fibonacci(1)의 호출 횟수를 구하는 것이다.
우리가 알고 있는 사실은 fibonacci(n)을 구하기 위해서는 fibonacci(n-1)와 fibonacci(n-2)을 더해야 한다는 점이다.
그렇다면 결국엔 fibonacci(n)을 호출한다면, 실행되는 fibonacci(0)과 fibonacci(1)은
'fibonacci(n-1)의 0과 1 호출 횟수' + 'fibonacci(n-2)의 0과 1 호출 횟수'와 동일하다는 뜻이다.
이 개념을 적용하여 문제를 풀어보자.
zero = [1, 0, 1]
one = [0, 1, 1]
우선, 각 숫자마다 0과 1의 호출 횟수를 저장할 리스트 zero, one을 생성해준다.
숫자가 0일 때 호출되는 0은 1번, 1은 0번이고,
숫자가 1일 때 호출되는 0은 0번, 1은 1번이다.
숫자가 2일 때 호출되는 0은 1번, 1은 1번이다. (fibonacci(2) = fibonacci(1) + fibonacci(0)이기 때문이다.)
이렇게 0부터 2까지는 미리 배열을 만들어서 이보다 큰 숫자에서의 0과 1의 호출 횟수를 추가로 저장하면 된다.
배열을 만들어서 값을 저장하는 이유는 '다이나믹 프로그래밍'을 통해 이미 구한 숫자를 또다시 구하는 일이 없도록 하여 시간을 단축시키기 위함이다.
def fibonacci(num):
length = len(zero)
if num >= length:
for i in range(length, num+1):
zero.append(zero[i-1] + zero[i-2])
one.append(one[i-1] + one[i-2])
print('{} {}'.format(zero[num], one[num]))
코드를 보면 배열의 길이를 구해서, 배열의 길이보다 입력받은 숫자의 값이 크거나 같으면 반복문을 시작한다.
(그렇지 않으면 이미 배열에 저장되어 있는 값을 출력하면 되기 때문이다.)
위에서 알아본 피보나치를 구하는
fibonacci(n) = fibonacci(n-1) + fibonacci(n-2) 개념을 적용하여,
'피보나치 n에서 0, 1의 호출횟수 = (피보나치 n - 1에서 0, 1 호출횟수) + (피보나치 n - 2에서 0, 1 호출횟수)' 을 계산하여 새로운 값을 배열에 추가한다.
이처럼 배열에 추가하여 동일한 작업을 없애면 시간을 단축시킬 수 있다.
T = int(input())
for _ in range(T):
fibonacci(int(input()))
그러고 나서 몇 번 반복할지를 변수 T에 입력받고 T번 만큼 피보나치 함수를 실행시킨다.
그럼 문제를 성공적으로 풀었음을 확인할 수 있을 것이다.
전체 소스 코드
zero = [1, 0, 1]
one = [0, 1, 1]
def fibonacci(num):
length = len(zero)
if num >= length:
for i in range(length, num+1):
zero.append(zero[i-1] + zero[i-2])
one.append(one[i-1] + one[i-2])
print('{} {}'.format(zero[num], one[num]))
T = int(input())
for _ in range(T):
fibonacci(int(input()))
👍클릭으로 구독하기👍
(이해가 다소 힘들거나, 틀린 부분이 있다면 댓글 부탁드리겠습니다! 😊)
💖도움이 되셨다면 '구독'과 '공감' 부탁드립니다!💖
'백준' 카테고리의 다른 글
| [백준 - Python] 2839번 : 설탕 배달 (1) | 2022.09.20 |
|---|---|
| [백준 - Python] 2671번 : 잠수함식별 (0) | 2022.09.14 |
| [백준/파이썬] 1004번 문제 '어린 왕자' (14) | 2021.06.11 |
| [백준/파이썬] 1002번 문제 '터렛' (10) | 2021.06.09 |
| [백준/파이썬] 1000번 문제 'A+B' (28) | 2021.06.08 |
![[백준/파이썬] 1003번 문제 '피보나치 함수'](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FHn8YQ%2Fbtq6RIHbGgq%2Fz7Go537xIDNQvpNh7KOPQ1%2Fimg.png)