
https://www.acmicpc.net/problem/1002
1002번: 터렛
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
www.acmicpc.net
문제
조규현과 백승환은 터렛에 근무하는 직원이다. 하지만 워낙 존재감이 없어서 인구수는 차지하지 않는다. 다음은 조규현과 백승환의 사진이다.

이석원은 조규현과 백승환에게 상대편 마린(류재명)의 위치를 계산하라는 명령을 내렸다. 조규현과 백승환은 각각 자신의 터렛 위치에서 현재 적까지의 거리를 계산했다.
조규현의 좌표 (x1, y1)와 백승환의 좌표 (x2, y2)가 주어지고, 조규현이 계산한 류재명과의 거리 r1과 백승환이 계산한 류재명과의 거리 r2가 주어졌을 때, 류재명이 있을 수 있는 좌표의 수를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 이루어져 있다.
한 줄에 x1, y1, r1, x2, y2, r2가 주어진다. x1, y1, x2, y2는 -10,000보다 크거나 같고, 10,000보다 작거나 같은 정수이고, r1, r2는 10,000보다 작거나 같은 자연수이다.
출력
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
예제 입력
 |
 |
문제 풀이
이 문제는 두 원의 중심과 반지름을 입력했을 때, 두 원 사이의 접점의 개수를 구하는 문제이다.
따라서 원의 중심 좌표 (x, y) 2쌍이 주어졌을 때, 두 좌표 사이의 거리를 구하는 공식을 알아야 한다.
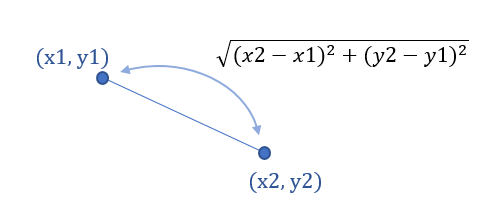
위 그림에 있는 식이 두 좌표 사이의 거리를 구하는 공식이다.
공식에 원의 중심 좌표를 대입하면 두 원 사이의 중심 거리(distance)를 구할 수 있다.
추가적으로 두 원의 위치 관계에 대해서도 알아야 한다.
해당 내용에 대해서는 아래에 있는 글을 참고하기 바란다.
- 만나지 않는 경우 (접점이 0개인 경우)



- 접하는 경우 (접점이 1개인 경우)

- 두 점에서 만나는 경우 (접점이 2개인 경우)

- 두 원이 겹치는 경우 (접점이 무수히 많은 경우)

두 원의 위치 관계를 알고 있으면 특정 조건에서 두 원의 접점 개수를 알아낼 수 있다.
이제 이 개념을 코드로 구현해보자.
전체 소스 코드
import math
T = int(input())
for _ in range(T):
x1, y1, r1, x2, y2, r2 = list(map(int, input().split()))
# 두 원의 중심 사이의 거리
dis = math.sqrt((x1 - x2)**2 + (y1 - y2)**2)
if dis == 0: # 두 원의 중심이 같을 경우
if r1 == r2: # 두 원의 크기가 같아 겹치는 경우
print(-1)
else: # 한 원이 다른 원 안에 들어가 있는 경우
print(0)
else: # 두 원의 중심이 다를 경우
if r1+r2 == dis or abs(r2-r1) == dis:
print(1)
elif ((abs(r1-r2) < dis) and (dis < r1+r2)):
print(2)
else:
print(0)
우선 테스트 케이스의 개수를 변수 T에 입력받고, for문을 통해 T만큼 반복하도록 한다.
for문에는 조규현, 백승환 터렛의 (x, y)좌표, 그리고 두 사람과 마린(류재명) 사이의 거리(r)를 입력 받는다.
# 두 원의 중심 사이의 거리
dis = math.sqrt((x1 - x2)**2 + (y1 - y2)**2)
그리고 조규현과 백승환의 터렛 좌표 사이의 거리를 구해준다.
위에서 설명했던 두 원의 중심 사이의 거리를 구하는 공식을 코드로 구현한 것이다.
이제 이 거리와 반지름 값을 비교하며 접점을 출력하면 된다.
if dis == 0: # 두 원의 중심이 같을 경우
if r1 == r2: # 두 원의 크기가 같아 겹치는 경우
print(-1)
else: # 한 원이 다른 원 안에 들어가 있는 경우
print(0)
else: # 두 원의 중심이 다를 경우
if r1+r2 == dis or abs(r2-r1) == dis:
print(1)
elif (r1+r2 > dis) and (dis > abs(r1-r2)):
print(2)
else:
print(0)
· 두 원의 중심이 같은 경우 / if d== 0 ·
 |
 |
위 조건에서 반지름까지 같다면 두 원은 겹친다는 뜻이 되므로 마린(류재명)이 있을 수 있는 위치는 무한대로 존재한다.
그렇지 않다면 하나의 원이 다른 원 안에 포함되어 있는 것이기 때문에 겹치는 부분이 없어 접점이 0개가 된다.
즉, 동심원인 경우이다.
· 두 원의 중심이 다른 경우 / if d != 0 ·
 |
 |
원의 중심이 다르다는 것은 두 원이 각각 다른 위치에 존재한다는 뜻이다.
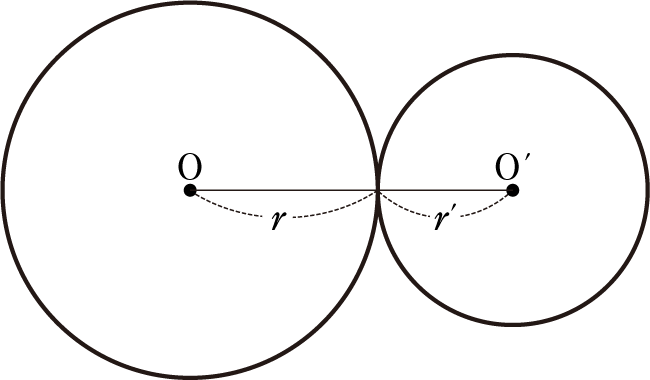
만약 접점이 1개라면 이렇게 외부에서 접하는 '외접'과 내부에서 접하는 '내접'이 있을 것이다.
이런 경우에는 두 반지름의 합이 중심 거리와 같거나 (r + r' == d),
두 반지름의 차가 중심거리와 같은 경우 (r1 - r2 == d) 이다.
· 두 점에서 만나는 경우 ·

만약 이렇게 접점이 2개가 생기는 경우에는 두 반지름의 합(r + r')이 중심 거리(d)보다 큰 경우이다.
단, 여기서 주의해야할 점은 중심 거리(d)가 두 반지름의 차(r - r')보다는 커야한다는 점이다.
그렇지 않으면 내접의 조건과 다를 바가 없어지기 때문이다.
이 외의 경우에는 모두 접점이 없으므로 0으로 출력해주면 문제 풀이는 끝이 난다.
👍클릭으로 구독하기👍
(이해가 다소 힘들거나, 틀린 부분이 있다면 댓글 부탁드리겠습니다! 😊)
💖도움이 되셨다면 '구독'과 '공감' 부탁드립니다!💖
'백준' 카테고리의 다른 글
| [백준 - Python] 2839번 : 설탕 배달 (1) | 2022.09.20 |
|---|---|
| [백준 - Python] 2671번 : 잠수함식별 (0) | 2022.09.14 |
| [백준/파이썬] 1004번 문제 '어린 왕자' (14) | 2021.06.11 |
| [백준/파이썬] 1003번 문제 '피보나치 함수' (16) | 2021.06.10 |
| [백준/파이썬] 1000번 문제 'A+B' (28) | 2021.06.08 |
![[백준/파이썬] 1002번 문제 '터렛'](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FJkm1e%2Fbtq6Mbo8fIZ%2FAAAAAAAAAAAAAAAAAAAAADrmqhUqZ8vNXP_06AAHukWLegYGlu1vrRdbpDp8HUN9%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DHwDZzVrCZ%252BKa0TI41dhy7Rn4qRg%253D)