[인공지능][개념] 합성곱 신경망(CNN) - 패딩(Padding)과 스트라이드(Strides), 풀링(Pooling) 완전정복하기

 

 

합성곱 신경망 (CNN - Convolutional Neural Network)

---

 

 

합성곱 신경망(CNN)은 이미지 데이터를 분류할 때 효과적인 딥러닝이다.

예를 들어, 숫자 이미지를 학습시켜 무슨 숫자인지를 맞춘다거나, 여러 옷 이미지 중에서 어떤 카테고리에 속하는 의류인지 맞추는 모델을 만들 수 있다.

합성곱(Convolution)은 마치 입력 데이터에 도장을 찍어 유용한 특성만 드러나게 하는 것으로 비유할 수 있다.

이번 글에서는 합성곱의 동작 원리에 대해 알아보겠다.

 

 

'각 특성에 뉴런의 가중치(w)를 곱하고 절편 더하여 결과 출력'

 

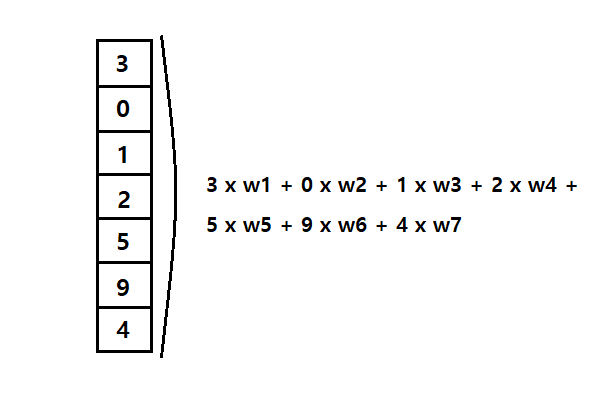
이전 포스팅에서 알아본 인공 신경망(ANN) 밀집층에는 뉴런마다 입력 개수만큼 가중치가 존재했다.

즉, 모든 입력에 가중치를 곱하는 셈이다.

인공 신경망은 처음에 가중치와 절편을 랜덤하게 초기화한 다음 에포크를 반복하며,

경사 하강법 알고리즘을 사용하여 손실이 낮아지도록 최적의 가중치와 절편을 찾아간다.

 

예를 들어, 밀집층에 뉴런이 3개 존재한다면 입력 개수에 상관없이 출력 또한 3개로 동일하다.

패션 MNIST 이미지에 있는 픽셀 784개를 입력받는 은닉층의 뉴런 개수가 100개면 각 뉴런은 100개씩 출력하여

총 784 * 100 = 78,400개의 모델 변수(Params)를 만들어낸다.

 

---

 

 

하지만 합성곱은 밀집층의 계산과는 조금 다르다.

입력 데이터 전체에 가중치를 적용하는 것이 아닌, 일부에만 가중치를 곱한다.

이게 무슨 말인지 아래 글을 통해 이해해보자!

 

'각 특성에 뉴런의 가중치(w)를 곱하고 절편을 더하여 1개의 결과 출력'

 

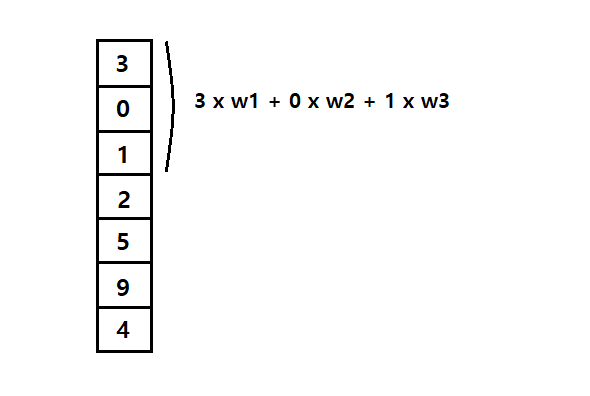
가중치 w1 ~ w3이 처음 3개 특성과 곱해져 1개의 출력을 만들어낸다.

그다음 뉴런이 한 칸 아래로 이동하여 w2 ~ w4 특성과 곱해져 새로운 출력을 만들어낸다.

바로 아래 그림처럼 말이다.

 

 

 

처음 1개의 출력에 이어 뉴런이 아래로 이동하여 또 다른 출력을 만들어내고 있다.

이렇게 한 칸씩 아래로 이동하면서 출력을 만들어내는 것이 합성곱이다.

인공신경망이었다면 출력이 8개였겠지만,

합성곱에서는 뉴런의 가중치(w)가 3개이기 때문에 위 과정을 거치면 결과적으로 5개의 출력이 만들어진다.

 

앞서 설명한 도장을 찍어 유용한 특성만을 드러나게 한다는 말이 바로 여기서 나타난다.

3칸짜리 도장(!)으로 입력 데이터 위를 하나씩 찍어 나가면서 결과를 만들어내는 것이다.

 

 

 

 

합성곱 신경망에서는 뉴런을 필터(filter) 혹은 커널(kernel)이라고 부른다.

위 그림에서의 필터를 도장으로 이해하면 되고, 입력 데이터를 필터로 찍어나가면서 출력을 만든다.

 

이 과정을 그림으로 설명하면 아래와 같다.

 

'입력 데이터 9개를 필터의 9개의 가중치와 곱하여 1개의 결과 출력'

 

 

입력 데이터 9개를 커널에 존재하는 9개의 가중치와 모두 곱하여 1개의 출력을 만들어낸다.

마치 도장을 찍듯이 말이다.

 

 

 

 

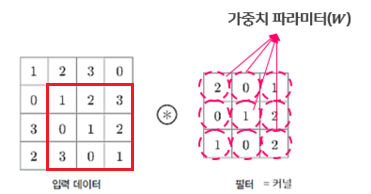그다음 오른쪽으로 이동하여 또다시 커널도장을 찍어 새로운 결과를 만들어 낸다.

더 이상 오른쪽으로 이동할 수 없으면, 아래로 한 칸 이동하여 다시 왼쪽에서부터 합성곱을 수행한다.

그럼 3 x 3 크기의 커널 도장이 총 4개의 결과를 출력할 것이다.

 

 

'3 x 3 크기의 커널로 만들어 낸 (3, 3, 4) 형태의 특성맵'

 

 

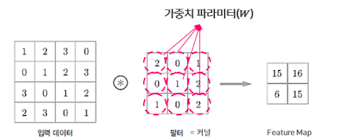
이렇게 합성곱 계산을 통해 얻은 출력을 특성맵(feature map)이라는 용어로 부른다.

여기에서는 3 x 3 크기의 출력이 4개이므로 특성맵의 형태(shape)는 (2, 2, 4)가 된다.

 

 

 

패딩(Padding)과 스트라이드(Strides)

---

 

 

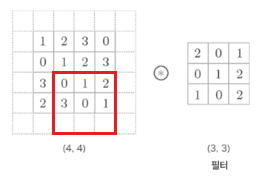
위에서 우리는 (4, 4) 크기의 입력에 (3, 3) 크기의 커널도장을 찍어가며 (2, 2) 크기의 특성맵 4개를 만들어냈다.

그런데 만약 커널도장의 크기는 (3, 3)으로 유지하고 출력의 크기를 입력의 크기 (4, 4)와 동일하게 만들려면 어떻게 해야 할까?

 

 

'(4, 4) 크기의 입력 데이터를 패딩(padding)한 (6, 6) 크기의 입력 데이터'

 

(4, 4) 입력과 동일한 크기의 출력을 만들기 위해서는 마치 '더 큰 입력에 합성곱을 하는 척' 해야 한다.

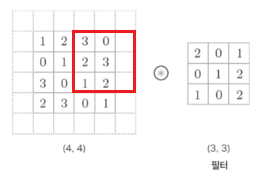
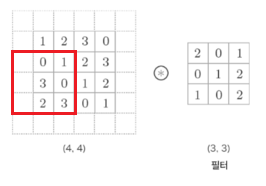
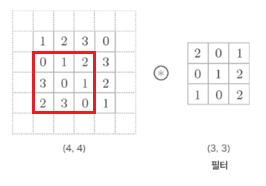
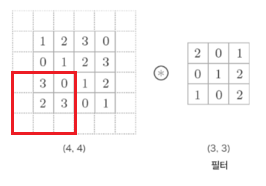
예를 들어, 위 그림처럼 실제 입력의 크기는 (4, 4)이지만 (6, 6)으로 만들어 다룬다고 가정해보자.

이 입력 데이터를 (3, 3) 크기의 커널 도장으로 찍어내 보자!

 

 

 

 

 

그럼 위와 같이 왼쪽 위에서 오른쪽 아래까지 한 칸씩 이동하면서 합성곱을 수행하며

입력과 같은 (4, 4) 크기의 출력을 만들 수 있다.

 

 

 

 

결과를 확인해보면 실제 입력 데이터의 크기였던 (4, 4)와 출력 데이터의 크기가 같은 것을 확인할 수 있다.

이렇게 입력 배열의 주위를 가상의 원소로 채우는 작업을 패딩(padding)이라고 부른다.

실제 입력값은 아니기 때문에 패딩은 0으로 채운다.

따라서 패딩을 사용하면 계산에 영향을 미치지 않으면서 입력과 출력 데이터의 크기를 동일하게 만들 수 있는 것이다.

 

이렇게 입력과 특성맵의 크기를 동일하게 만들기 위해 주위에 0으로 패딩하는 것을 세임 패딩(Same padding)이라고 부르고,

패딩 없이 순수한 입력 배열에서만 합성곱을 하여 특성 맵을 만드는 경우를 밸리드 패딩(Valid padding)이라고 부른다.

 

 

''' 그런데 왜 합성곱에서 패딩을 사용해야 하는 것일까? '''

 

 

 

 

이 합성곱 과정에서 배열의 맨 왼쪽 위 모서리에 위치한 '1' 을 주목해보자.

만약 패딩이 없다면 위 그림에서 (4, 4) 크기의 입력에 커널 도장은 처음에 딱 한 번만 찍히게 된다.

예시로 1을 언급했지만, 사실상 모서리에 있는 다른 3개의 값도 마찬가지이다.

 

반면 다른 원소들은 2번 이상의 커널 도장이 찍혀 계산된다.

만약 이 입력이 이미지라고 생각했을 때, 모서리에 중요한 정보가 있다면 해당 정보는 특성맵에 잘 전달되지 않을 것이다.

왜냐?! 도장이 한 번밖에 안 찍혔다는 것은 사실상 가중치와 한 번밖에 곱해지지 않았다는 뜻이기 때문이다.

 

이렇게 패딩을 하지 않으면 중앙부와 모서리 픽셀이 합성곱에 기여하는 비율에 큰 차이가 발생한다.

그러나 만약 2픽셀을 패딩해주면 중앙부와 모서리에 위치한 픽셀이 합성곱에 기여하는 비율이 1 : 1로 동일해진다.

 

이처럼 적절한 패딩은 이미지 주변에 있는 중요한 정보를 잃어버리지 않도록 도와준다.

 

 

---

 

 

지금까지 알아본 합성곱은 상하좌우로 한 칸씩 이동하였다.

이것은 스트라이드(strides)가 1이기 때문이다.

만약 두 칸씩 건너뛰고 싶다면 스트라이드(strides)를 2로 설정해주면 된다.

단, 두 칸씩 이동하게 되면 커널 도장을 찍는 횟수가 줄어드는 만큼, 만들어지는 특성 맵의 크기는 더 작아질 것임을 알고 있어야 한다.

파이썬의 케라스에서는 스트라이드의 가로/세로로 이동하는 크기를 튜플(tuple)로 각각 지정해줄 수 있는데,

웬만하면 가로 세로/세로 이동 크기를 다르게 지정하는 경우는 거의 없으며, 1보다 크게 스트라이드를 사용하는 경우도 드물다고 한다.

 

 

 

풀링(Pooling)

---

 

 

풀링(Pooling)은 합성곱 층에서 만든 특성맵의 가로세로 크기를 줄이는 역할을 수행한다.

예를 들어 (2, 2, 3) 크기의 특성맵에 풀링을 적용하면 특성맵의 개수는 그대로 유지하고

너비와 높이만 줄어들어 (1, 1, 3) 크기의 특성맵이 만들어진다.

 

풀링도 합성곱처럼 특성맵 위를 지나가면서 도장을 찍는다.

도장을 찍은 영역에서 가장 큰 값을 고르거나, 평균값을 계산하는데

이를 각각 최대 풀링(Max Pooling)과 평균 풀링(Average Pooling)이라고 부른다.

 

이해를 돕기 위해, (4, 4) 크기의 특성맵을 (2, 2) 최대 풀링(Max Pooling)을 적용하여 크기를 줄여보자.

 

 

 

'최대 풀링(Max Pooling)을 적용하여 (2, 2)로 줄인 특성맵'

 

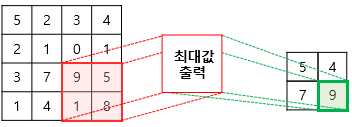
왼쪽에 위치한 (4, 4) 크기의 특성맵에서 최댓값을 출력하는 (2, 2) 도장을 2칸씩 이동하며 찍는다.

(풀링은 풀링 크기만큼 stride가 지정되기 때문에 (2, 2) 풀링에서는 stride가 2로 설정된다.)

최대 풀링은 가장 큰 값을 고르기 때문에 (2, 2) 영역에서 5를 고르고,

그다음 4, 7, 9를 차례대로 골라 (2, 2) 크기의 출력을 만든다.

특성맵이 여러개라면 동일한 작업을 반복한다.

즉, 특성맵이 10개 존재하는 (4, 4, 10) 형태의 특성맵이라면, 풀링 또한 10번 반복하여 (2, 2, 10) 형태가 된다.

 

 

평균 풀링(Average Pooling) 또한 동일하게 특성맵 위에서 이동하며 차례로 도장을 찍어나간다.

단, 최대 풀링과 다르게 특성 맵에 있는 값 중에 최댓값을 고르는 것이 아니라 평균을 구하여 특성맵을 줄여나간다.

 

 

'최대 풀링(Max Pooling)과 평균 풀링(Average Pooling)의 차이'

 

 

그림을 확인해보면, 최대 풀링과 다르게 (2, 2) 만큼 묶어서 평균을 구하여 특성맵을 줄이고 있다.

최댓값 대신 평균을 계산하는 것만 빼면 최대 풀링과 동일하다.

알아두어야 할 것은 많은 경우에서 평균 풀링보다 최대 풀링을 많이 사용하는데,

그 이유는 평균 풀링은 특성 맵에 있는 중요한 정보를 평균하기 때문에 정보가 희석될 수도 있기 때문이다.

 

 

---

 

이번 포스팅에서는 합성곱 층, 필터, 패딩, 스트라이드, 풀링 등 합성곱 신경망의 전체적인 개념에 대해 알아보았다.

다음 글에서는 해당 글에 대한 이론을 직접 파이썬 코드로 구현해보도록 하겠다.

 

 

 

👍클릭으로 구독하기👍

 

 

(이해가 다소 힘들거나, 틀린 부분이 있다면 '댓글' 부탁드리겠습니다! 😊)

💖도움이 되셨다면 '구독'과 '공감' 부탁드립니다!💖