![[인공지능][개념&실습] 차원 축소 알고리즘 - 주성분 분석(PCA)을 알아보고 사진의 크기를 줄여보자](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FLdqo9%2Fbtq5HLKfGuV%2FzKQW9EhlzLKgdPCGl354r1%2Fimg.jpg)
차원 축소
우리는 지난 포스팅에서 K-Means(++) 알고리즘을 사용하여 이미지를 비지도 학습으로 분류해보는 시간을 가져 보았다.
하지만 여기에는 한 가지 문제점이 존재한다.
우리가 이전 시간에 사용했던 이미지는 100px * 100px로, 총 10,000개의 픽셀로 이루어진 이미지였다.
즉, 하나의 이미지에는 10,000개의 차원(특성)이 존재한다는 것이다.
(머신러닝에서는 특성을 차원(Dimension)이라고도 부른다.)
이게 정확히 무슨 뜻인지 사진을 통해 알아보자.
예시를 위해 가져온 자몽 이미지이다. 🍊
그냥 봤을 땐 그냥 이미지이지만 이 이미지를 확대해보면 . . .
이제는 이미지에서 자잘자잘한 픽셀들이 눈에 들어올 것이다.
학습을 하는 모델에게는 이런 픽셀 하나하나가 각각의 특성이 되며, 이 픽셀들을 모두 학습을 위한 데이터로 사용하게 된다.
앞서 알아본 바와 같이 이렇게 특성이 많으면 모델은 훈련 데이터에 쉽게 과대 적합될 뿐만 아니라,
학습 데이터를 보관하는 데에 있어 저장 용량이 크게 부족해지는 단점이 발생한다.
이런 문제를 해결하기 위해 등장한 것이 바로 비지도 학습 작업 중 하나인 차원 축소 알고리즘이다.
그중에서도 우리는 주성분 분석(PCA)을 알아볼 것이다.
주성분 분석(PCA)
주성분 분석(PCA)은 데이터에 있는 분산이 큰 방향을 찾는 것으로 이해할 수 있다.
분산이란 데이터가 널리 퍼져 있는 정도를 말한다.
즉, 분산이 큰 방향을 데이터로 잘 표현하는 벡터로 생각할 수 있다.
예를 들어 이런 형태의 데이터 그래프가 있다고 생각해보자.
이 데이터는 완전히는 아니지만 우측 상단 방향으로 대각선이 길게 늘어진 형태를 띠고 있다.
이 데이터에서 가장 분산이 큰 방향은 어디일까?
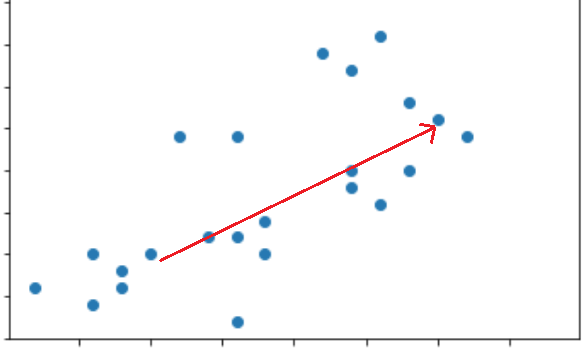
직관적으로 우리는 길게 늘어진 대각선 방향으로 분산이 가장 크다고 알 수 있다.
위 그래프에서 화살표의 방향이 왼쪽 아래를 향하든, 오른쪽 위를 향하든 크게 의미가 없다.
중요한 것은 분산이 큰 방향을 찾는 것이다.
이 직선이 원점에서 출발한다면 이 그림에서처럼 두 원소로 이루어진 벡터로 표현할 수 있을 것이다.
이 벡터를 주성분(Principal Component)이라고 부르며, 이 주성분 벡터는 원본 데이터에 있는 어떠한 방향이다.
따라서 주성분 벡터의 원소 개수는 원본 데이터셋에 있는 특성 개수와 같다.
방금 찾은 첫 번째 주성분(벡터)를 찾았다면, 두번째 주성분을 찾아야 한다.
주성분을 찾는 원리는 이전 주성분(벡터)에 수직이며, 분산이 가장 큰 방향의 벡터를 찾는 것이다.
그럼 계속해서 다음 주성분을 찾아보자.
이 그림처럼 두번째 주성분은 첫번째 벡터에 수직이면서 분산이 가장 큰 방향으로 늘어져 있다.
여기서는 2차원이기 때문에 수직인 두 번째 주성분의 방향은 하나뿐이다.
(일반적으로 주성분은 원본 특성의 개수만큼 찾을 수 있다.)
지금까지 주성분의 특징에 대해 알아보았으니, 코드를 통해 과일 사진 데이터를 직접 주성분 분석해보자.
!wget https://bit.ly/fruits_300_data -O fruits_300.npy
import numpy as np
fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)
우선, 저번 포스팅처럼 !wget 명령어를 통해 사과, 바나나, 파인애플로 이루어진 과일 데이터를 불러온다.
마찬가지로 100px * 100px 모양의 과일 이미지 데이터를 10,000px로 펼쳐준다.
지난 포스팅 참고 :
([인공지능][개념] K-Means 알고리즘의 문제점과 'K-Means++ 클러스터링'을 통해 개선하기 : https://itstory1592.tistory.com/19)
from sklearn.decomposition import PCA
pca = PCA(n_components=50)
pca.fit(fruits_2d)
print(pca.components_.shape)
그다음엔 사이킷런에서 제공하는 PCA 클래스를 임포트하여 생성해주는데,
이때 n_components를 50으로 입력하여 주성분 개수를 50개로 설정해준다.
그리고 해당 pca 인스턴스의 components의 데이터 형태를 출력해보자.
배열의 첫 번째 숫자는 우리가 입력한 주성분의 개수를 의미하고,
두 번째 숫자는 원본 데이터의 특성 개수를 의미한다.
총 10,000개의 픽셀이었으므로 원본 데이터의 특성은 10,000개인 것이다.
import matplotlib.pyplot as plt
def draw_fruits(arr, ratio=1):
n = len(arr) # n은 샘플 개수입니다
# 한 줄에 10개씩 이미지를 그립니다. 샘플 개수를 10으로 나누어 전체 행 개수를 계산합니다.
rows = int(np.ceil(n/10))
# 행이 1개 이면 열 개수는 샘플 개수입니다. 그렇지 않으면 10개입니다.
cols = n if rows < 2 else 10
fig, axs = plt.subplots(rows, cols,
figsize=(cols*ratio, rows*ratio), squeeze=False)
for i in range(rows):
for j in range(cols):
if i*10 + j < n: # n 개까지만 그립니다.
axs[i, j].imshow(arr[i*10 + j], cmap='gray_r')
axs[i, j].axis('off')
plt.show()
이 코드 또한 이전 포스팅에서 언급된 내용이다.
한 줄에 최대 10개씩 과일 이미지를 출력하는 메소드를 사용자 정의 함수로 구현한 것이다.
draw_fruits(pca.components_.reshape(-1, 100, 100))
위에서 정의한 메소드로 과일의 컴포넌트를 그림으로 그려보자.
draw_fruits() 메소드의 axs.imshow()에는 픽셀을 펼쳐놓은 데이터가 아닌, 가로 세로 형태의 데이터로 제공해주어야 한다.
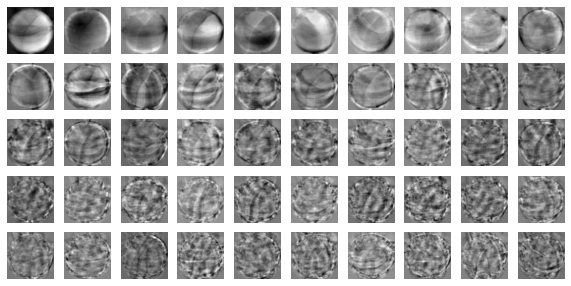
그럼 이렇게 주성분 50개가 출력된다.
이 주성분은 원본 데이터에서 가장 분산이 큰 방향을 순서대로 나타낸 것이다.
즉, 데이터셋에 있는 어떤 주요한 특징을 잡아낸 것처럼 생각할 수도 있다.
그럼 이제 훈련을 마친 pca를 통해, 우리가 가지고 있는 과일 이미지를 PCA의 transform() 메소드를 사용하여 원본 데이터 차원을 50으로 줄여보는 실습을 해보자.
#주성분 분석 이전 shape
print(fruits_2d.shape)
#주성분 분석 이후 shape
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)
주성분 분석 이전의 데이터 형태를 살펴보면, 300개의 데이터로 10,000개의 차원을 가지고 있지만
변형 이후에는 300개의 데이터를 그대로 유지하면서 50개의 차원으로 줄어든 모습을 확인할 수 있다.
그럼 변형된 데이터를 원본 데이터로 복구시키는 것도 가능할까?
당연히 가능하다.
10,000개의 특성을 50개로 줄이는 과정에서 어느 정도 손실이 발생할 수 있겠지만, 최대한 분산이 큰 방향으로 데이터를 투영했기 때문에 원본 데이터의 상당 부분을 재구성할 수 있다.
PCA 클래스에서는 이런 의문을 해결하기 위해 inverse_transform() 이라는 메소드를 제공해준다.
우리가 변형시킨 fruits_pca 데이터를 전달하여 10,000개의 특성을 복원해보자.
fruits_inverse = pca.inverse_transform(fruits_pca)
print(fruits_inverse.shape)
fruits_reconstruct = fruits_inverse.reshape(-1, 100, 100)
예상대로 10,000개의 특성이 복원되었다.
이 데이터를 다시 100 * 100 크기의 데이터 형태로 변형시킨 후 출력해보겠다.
for start in [0, 100, 200]:
draw_fruits(fruits_reconstruct[start:start+100])
print("\n")
 |
 |
 |
100개의 데이터씩 출력해본 결과 거의 모든 과일이 잘 복원되었다는 것을 확인하였다.
이전에 비해 일부 흐려지거나 번진 부분이 있지만, 50개의 특성을 10,000개로 늘린 것을 감안한다면 완벽하게 복원된 것이나 다름없다고 말할 수 있다.
그런데 여기서 한 가지 의문이 생길 수 있는데,
과연 우리가 만든 주성분 50개는 과연 얼마나 많은 분산을 보존하고 있을까?
설명된 분산(Explained Variance)
주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값을 설명된 분산(explained variance)이라고 한다.
PCA 클래스에서는 explained_variance_ratio_라는 변수에 접근하면 50개의 주성분 각각이 가지고 있는 분산 비율을 확인해볼 수 있다.
이 분산 비율을 모두 더하면 50개의 주성분으로 표현하고 있는 총 분산의 비율을 얻을 수 있다.
직접 코드를 통해 알아보자.
print(np.sum(pca.explained_variance_ratio_))
plt.plot(pca.explained_variance_ratio_)
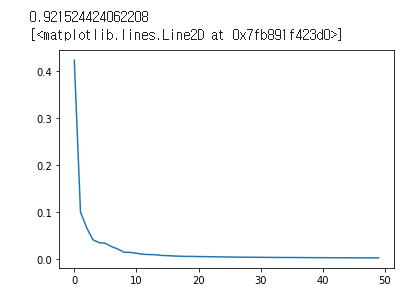
넘파이(numpy)의 sum() 메소드를 통해 pca의 설명된 분산 데이터의 합계를 구해서 출력해보면,
총 50개의 주성분이 원본 데이터의 92%를 나타내고 있다고 말해준다.
이를 그래프로 표현해보면, X축에는 주성분, Y축에는 설명된 분산으로 이루어진 그래프가 나타난다.
당연하게도 첫 번째 주성분이 40% 정도의 대부분의 분산을 포함하고 있으며,
10개 이후부터는 각 주성분이 설명하고 있는 분산이 매우 작음을 알 수 있다.
그럼 이 주성분 50개를 K-평균 알고리즘과 함께 사용해보면 어떨까?
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_pca)
print(np.unique(km.labels_, return_counts=True))
확인해보기 위해 3개의 클러스터로 이루어진 KMeans 객체를 생성하고, 주성분 50개로 이루어진 과일 이미지 데이터를 훈련시킨다.
그리고 각 label에 해당하는 원소 개수를 출력해보면 다음과 같은 결과가 출력될 것이다.
이 배열을 시각화하여 이미지가 어떤 식으로 나누어졌는지 확인해보자.
for label in range(0, 3):
draw_fruits(fruits[km.labels_ == label])
print("\n")
 |
 |
 |
주성분 50개로 분류한 결과 꽤 높은 정확도로 이미지가 나누어졌다.
이미지처럼 특성이 여러 개일 경우에는, 데이터를 그래프로 시각화하기가 어렵다.
하지만 주성분을 2개로 축소한다면 가능하지 않을까?
설명된 분산 그래프에서 확인했듯이, 주성분 초반 부분에 대부분의 분산을 포함하고 있다.
그렇기 때문에 특성이 2개일 때에도 데이터를 분류하는 데에 있어 큰 영향을 미치지 않을 것이다.
위에서 작성한 코드의 PCA클래스 매개변수인 n_components를 2로 설정하여 모델을 다시 훈련을 시키고,
아래의 코드를 통해 이미지 데이터를 산점도로 표현해보자.
for label in range(0, 3):
data = fruits_pca[km.labels_ == label]
plt.scatter(data[:,0], data[:,1])
plt.legend(['apple', 'banana', 'pineapple'])
plt.show()
정말 보기 쉽게 3종류의 과일이 잘 분류되었음을 눈으로 확인해볼 수 있다.
이처럼 차원 축소를 했을 때의 장점은 용량을 낮출 수 있을 뿐만 아니라, 특성을 2개 이하로 만들어 X축 Y축으로 지정하여 데이터의 분류된 모습을 쉽게 시각화할 수 있다는 점이다.
아래에는 차원 축소의 장점에 대해 정리하며 포스팅을 마무리하겠다.
차원 축소의 장점 : 특성이 많으면 선형 모델의 성능이 높아지고 훈련 데이터에 쉽게 과대 적합되는 경향을 보이는데, 차원 축소는 특성을 줄일 수 있으므로 모델의 과대 적합을 최소화할 수 있다.
전체 소스 코드 :
https://colab.research.google.com/drive/1rOVockfQZpNuL8fqR73mVZzSqgmkPqo7
(이해가 다소 힘들거나, 틀린 부분이 있다면 댓글 부탁드리겠습니다! 😊)
💖댓글과 공감은 큰 힘이 됩니다!💖